なぜ数字やグラフを使うのか?
数字で客観的に示す。
グラフで聞き手の理解を助ける。
これら、どちらもよく聞くフレーズです。確かに、データを示すうえで数字やグラフが聞き手に安心感を与え、理解を促す役割は大きいでしょう。
ですが、話し手が、わざわざ工夫してデータを提示するのには、そんな利他的な理由“だけ”でしょうか。
おそらく違いますよね。
実際の目的は、より利己的な要素である、話し手の主張を補強・正当化するという側面も含まれるはずです。さらに、その話し手の主張は、すべてが誠実なものとは限りません。
そこで、今回は、データを数字やグラフといった形で提示された際、そのデータを提示した相手の意図を理解うえで、重要なポイントを僅かながらご紹介いたします。
くれぐれも申し上げますが、何もデータサイエンティスト入門書ではないので、データの正確な解釈方法といった難しい話は致しません。話し手が、話し手の都合で提示したデータを、鵜呑みにしないためのお話になります。
ポイント1:そのデータどうやって集めました?
まず、初めにご紹介するのが、最初にして最悪の落とし穴 ― データの集め方になります。
例えば、電子機器の操作が大きなハードルとなる高齢の方に、街頭アンケートを取ったのと、オンラインアンケートを取ったのでは大きく異なる、というのはイメージがつきやすいでしょう。
- カタカタとパソコンを打ってアンケートに答えた80歳女性。
- もう一方は、普段パソコンやスマホは使わないが散歩中に突然声を掛けられ、会話を楽しみがてらアンケートに答えた80歳女性
このお二人の様子は全く異なりますが、どちらも80歳女性のアンケート回答として処理され、私たちに提示されうるのです。データで見ると些細な差ですが、現実世界なら大いなる人違いです。
そのため、誰が、いつ、どこで、誰に対して、どのような方法でアンケートをとったのか、といった、前提条件の確認が大変重要なのです。
しかしながら、これらのアンケートの前提条件という味気ない説明は、大概サラッと流されてしまいます。なぜなら、聞き手も話し手も、そんなことには興味がないからです。特に、話し手は、一応調査方法は~と、決まりごとのように軽く触れたり、グラフの端っこに書きますが、やはり取ったデータを見せることに必死になります。
だからこそ、たとえ不安を煽るようなデータを提示されたとしても、そのデータには自分自身も当てはまる話なのか、それを見極めるためにこそ、まずはデータがどう集められたのかに意識を向けることが、聞き手にとっても大前提なのです。
ポイント2:“平均的に“本当ですか?
次にご紹介するのが、平均という言葉の危険性です。
平均値を求める計算は、小・中学校で習うとおり、データの合計をデータの個数で割るだけであり、そのデータの上振れ下振れを無視した“データのあらまし“がわかる、便利なツールとして紹介されます。
特に、大きな規模のデータをもとに、平均的には○○といわれてしまうと、どこか納得してしまいますよね。ですが、実際には、平均値があまりあてにならないこともあるのです。
平均値が使えない?
下図をご覧ください。横軸は数値(value)、縦軸は人数(count)を表しています。
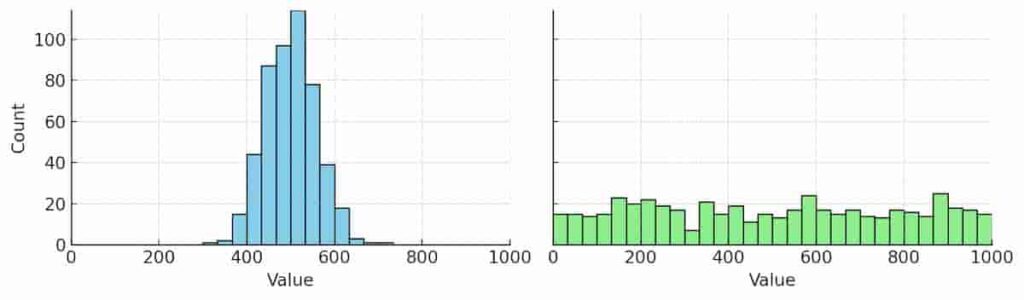
どちらのグラフも、合計人数は500人、数値の平均値は約500で揃え、それぞれ極端なケースとして作成しました。
左右を比べると、左図は数値500付近にとがった山があり、非常に多くの人が平均付近に集中していることがわかります。一方で、右図は小さな凸凹はありますが概ね平らに見え、すべての数値に対して満遍なく人が分布していることがわかります。
正直、このグラフ中の具体的な数値に意味はありません。グラフの形=データの散らばり方が重要なのです。
左図のように、多くの人の結果が大体同じような値に落ち着くグラフであれば、自分の結果も凡そその結果に近いものとなることが予想されるため、データから得られる平均値は非常に参考になります。一方で、右図のように多くの人の結果がランダムに散らばるグラフの場合、自分の結果もどこに散らかるのかわからないのですから、たとえその平均値がわかったところでさほど有用とは言えません。
言い換えますと、平均という言葉で丸め込まれないためには、データの散らばり具合を確認するということが重要なのです。
この実用例が、投資する際なんかに耳にするボラティリティです。ボラティリティという言葉は一般的には、一定期間でどれくらい平均損益が変動し得るかを値として表すもので、値動きの振れ幅を表します。つまり、年間ボラティリティが大きいと、去年は大儲け今年は大損といったように、値動きの激しいことがわかるのです。
それでは、過去のデータから
- 平均リターンが15%
- 年間ボラティリティが大きい
とされる対象に1年間投資する場合を想定すると、1年後に資産はどうなると考えるべきでしょうか。
過去から未来がどうなるかなんてわからないというご意見はごもっともですが、過去のデータを参考にすると、1年間投資した資産は、激減/激増し得ると考えるべきであり、15%という数字は絵にかいた餅として心構えしておくことが必要だとわかるわけです。
平均値よりも真ん中?
ちなみにもう少しお話しますと、平均値よりも、差のあるデータを順番に並べた時に中央に位置する値である中央値のほうが、より“データのあらまし“を表すことも少なくないのです。
下に図をお示しします。
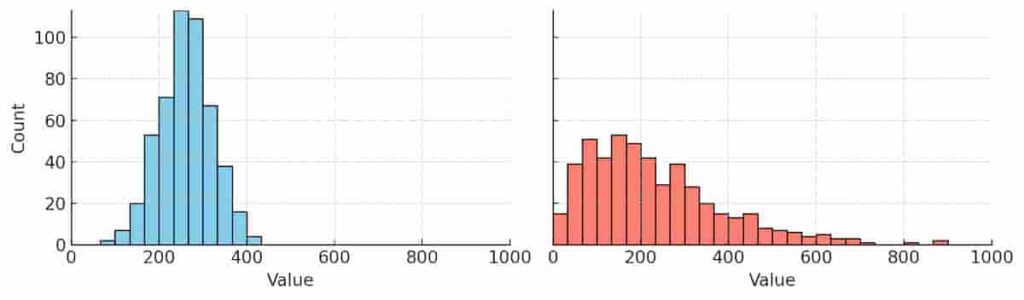
今回も、人数(Count)は500人ですが、平均値を250程度に設定しています。
左図は一個前の同色の左図のグラフとほぼ同じように、平均付近に集中しています。一方で右図はどうでしょう。数値(Value)の小さい部分に多くの人がまとまっているように見えますが、よくみると大多数からかなり外れた900あたりにもデータがあります。こういう場合、平均値を計算すると、その並外れた値が平均を引っ張ってしまう、つまり盛られすぎてしまうのです。
そこで、中央値(右図では、数値の大きい人から250人目の値と251人目の値の平均)を求めてみますと、約201とわかりました。
平均250と中央値201を比べますと、まだ中央値のほうがデータの厚みのある部位に位置しており、典型的な”真ん中”を表していることがわかります。
これが有用になるのが、例えば年収のデータです。厚生労働省の所得の分布状況に関する統計(R6 国民生活基礎調査概況)より、平均所得は536万円/年ですが、中央値は410万円/年と、100万円以上ずれがあることがわかります。なので、世の中の実感値が平均からずれることがあるのです。ほかにも、以前ご紹介した医療費に関しては、病弱・高齢の方に集中するという点で平均が実態とはずれうると考えられます。
”平均”の落とし穴にはご注意を!
さて、しばしば神格化される平均値においても、実は様々な落とし穴もあるわけです。
確かに世の中のデータは、平均値のあたりにとがった山があるデータが多いため、日常的に様々な種類のデータにでも触れていない限り、経験的に平均値=データの厚みのある真ん中の部分、と思ってしまうかもしれません。
ですが、これを逆手にとれば、当てにならない平均を提示して詐欺的な話につなげるのも容易ということです。
だからこそ、”平均”を鵜呑みにしないということ、そして少し余裕があれば、データ全体を見てみるというのが大切なのです。
まとめ
実は、全く専門的な内容にするつもりはなかったので、一つの記事で終わるかと思っておりました。ですが、いろいろな手口とその対応をご紹介しようと考えれば考えるほど長くなってしまったので、一旦ここまでとさせてください。
今回はデータの詳細な内容には触れずとも確認できる部分である、データの集め方、それからよく文字やトークで強調される平均に焦点を絞りました。
引き続き、続編にて、今回はご紹介できなかったデータの詳細である、データの範囲に関する重要なポイントをもう2つ、お伝えいたします。
最後までお読みいただきありがとうございました。
※本記事は公開データや一般的な考え方をもとに解説したものであり、特定の投資を推奨するものではありません。実際の判断にあたっては、必ずご自身で最新情報をご確認ください。